In this way a message which was
readable initially can be put in a form called cipher text that cant be
understood at a simple glance.
Julius Caesar, the Roman ruler,
used a very simple cipher for secret communication with his army generals. He substituted
each letter of the alphabet with a letter three positions further along.
The Caesar Cipher can be expressed in a more mathematical form as follows:
En(x) = (x+n) mod 26
In plain terms, this means that
the encryption of a letter x is equal to a shift of x + n, where n is the
number of letters shifted. The result of the process is then taken under modulo
division, essentially meaning that if a letter is shifted past the end of the
alphabet, it wraps around to the beginning.
Decryption of the encrypted text (ciphertext) would be defined
similarly, with instead a subtraction of the shift amount.
Dn(x) = (x-n) mod 26
Here is the python code for encrypting data stored in a local file input_file.txt and store the encrypted format in another local file called encrypt_file.txt and also has option to decrypt the ciphered text and put the resultant message into a local file decrypt_file.txt ,
import random
alphabet = "abcdefghijklmnopqrstuvwxyz"
key = random.randint(1, 26)
def encrypt():
position = list()
res = ""
f = raw_input("Enter your filename\n")
fhand = open(f,'r')
str = fhand.read()
fhand.close()
for i in range(len(str)):
position.append(alphabet.find(str[i]))
for i in range(len(str)):
if str[i] != " ":
position[i] = (position[i]+key)%26
res = res + alphabet[position[i]]
else: res = res + " "
fhand = open("encrypt_file.txt",'w')
fhand.write(res);
fhand.close()
def decrypt():
position = list()
res = ""
fhand = open("encrypt_file.txt",'r')
str = fhand.read()
fhand.close()
for i in range(len(str)):
position.append(alphabet.find(str[i]))
for i in range(len(str)):
if str[i] != " ":
position[i] = position[i]-key
if position[i] < 0:
position[i] = 26 + position[i]
res = res + alphabet[position[i]]
else: res = res + " "
fhand = open("decrypt_file.txt",'w')
fhand.write(res)
print res
fhand.close()
option = {1 : encrypt,
2: decrypt,
}
while(1):
print("menu:\n1. Encrypt a string\n2. decrypt a string\n")
choice = raw_input("enter your option\n")
option[int(choice)]()
ch = raw_input("Do you want to continue(1/0)")
if ch == '0':
break
else:
continue
The caesar cipher can be broken in milliseconds using
automated tools. since there are only 25 possible keys i.e. each possible shift
of the alphabet. we can try decrypting the ciphertext using each key and
determine the fitness of each decryption. this forms a solution as we know is
brute force and possible only for simple ciphering techniques like this
approach.
The crux of the approach depends on determining the fitness
of a piese of deciphered text. this is done by calculating the statistics of
the deciphered text and compare these statistics to those calculated from
standard english text. a fitness function will give us a number, the higher the
number the more likely the particular key is correct one. for this session we
will use quadgram statistics for better results as its probability to find the
exact result is higher than bigram and trigram statistics.
This method workds by first determininig the statistics of
english text. then calculating the likely hood that the ciphertext comes from
the same distribution. as incorrectly deciphered message will probably contain
sequences eg. ‘qkpc’ which are very rarre in normal english. in this way we can
rank decryption keys. the decryption key we want is the one that produces
deciphered text with fewest rare sequences.
If our cipher text is the following:
ymjhfjxfwhnumjwnxtsjtkymjjfwqnjxypstbsfsixnruqjxyhnumjwx
To find out what the original was, we try decryting a piece
of cipheredtext with each of the 25 possible keys, calculating fitness for each
trial decryption.
key
plaintext
fitness
------------------------------------------------------
1: xligeiwevgmtlivmwsrisjxliievpm..., -442.22
2: wkhfdhvduflskhulvrqhriwkhhduol..., -495.20
3: vjgecguctekrjgtkuqpgqhvjggctnk..., -484.13
4: uifdbftbsdjqifsjtpofpguiffbsmj..., -490.73
5: thecaesarcipherisoneoftheearli..., -246.02
6: sgdbzdrzqbhogdqhrnmdnesgddzqkh..., -485.69
7: rfcaycqypagnfcpgqmlcmdrfccypjg..., -481.17
8: qebzxbpxozfmebofplkblcqebbxoif..., -478.19
9: pdaywaownyeldaneokjakbpdaawnhe..., -415.66
10: oczxvznvmxdkczmdnjizjaoczzvmgd..., -488.75
11: nbywuymulwcjbylcmihyiznbyyulfc..., -490.46
12: maxvtxltkvbiaxkblhgxhymaxxtkeb..., -490.82
13: lzwuswksjuahzwjakgfwgxlzwwsjda..., -483.63
14: kyvtrvjritzgyvizjfevfwkyvvricz..., -475.01
15: jxusquiqhsyfxuhyieduevjxuuqhby..., -466.90
16: iwtrpthpgrxewtgxhdctduiwttpgax..., -458.49
17: hvsqosgofqwdvsfwgcbscthvssofzw..., -474.67
18: gurpnrfnepvcurevfbarbsgurrneyv..., -460.86
19: ftqomqemdoubtqdueazqarftqqmdxu..., -467.13
20: espnlpdlcntaspctdzypzqespplcwt..., -454.29
21: dromkockbmszrobscyxoypdrookbvs..., -461.91
22: cqnljnbjalryqnarbxwnxocqnnjaur..., -479.58
23: bpmkimaizkqxpmzqawvmwnbpmmiztq..., -473.52
24: aoljhlzhyjpwolypzvulvmaollhysp..., -474.57
25: znkigkygxiovnkxoyutkulznkkgxro..., -494.13
The fitness of each of the text is shown above, with text
corresponding to a key of 5 showing a much higher fitness than other possible
keys (it may be confusing because the scores are negative, here we chose the
least negative scoreas being the highest fitness.). we could have also tried
reading each sentence to find which one is readable but this becomes
impractical when there are many possible keys.
Quadgram statistics as fitness measure
When trying to break ciphers, its often useful to try
deciphering with many different keys, then look at the deciphered text. if the
text looks very like english we consider the key is a good one.
What we need is a way of determining if a piece of text is
very like english. this is achieved by counting quadgrams or group of 4
letters.
eg: for the text attack, quadgrams are: atta, ttac, and
tack.
To use quadgram to detemine how similar test is to english,
we first need to know which quadgrams occur in english. to do this we take a
large piece of text, for eaxmple several books worth of text, and count each of
quaddgrams that occur in them. we then divide these counts by the total number
of quadgrams encountered to find the probability of each.
If we count the quadgrams in tolstoy's "war and peace",
we have roughly 2,500,000 total quadgrams after all spaces and punctuation are
removed. the probability of a specific quadgram is calculated by dividing the
count of that quadgram by the total number of quadgrams in our training corpus.
the log probability is simply the logarithm of this number. a few specific
counts:
quadgram
count log probability
------------------------------------------------------
aaaa 1
-6.4001876
qkpc 0 -9.4001876
your 1132 -3.3463412
tion 4694 -2.7286445
atta 359 -3.8450932
The table above shows that some quadgrams occur much more
often than other quadgrams, this can be used to determine how similar to
english a specific piece of text is. if the text contains qpkc, it is probably
not english, but if it contains tion, it is much more likely to be english.
To compute the probability of a piece of text being english,
we must extract all the quadgrams, then multiply each of the quadgram
probabilities.
For the text attack, the quadgrams are atta, ttac, and tack.
the total probability is
where e.g.
In the equation above, count is the number of times the
quadgram occured, n is the total number of quadgrams in the training sample.
When multiplying many small probabilities, numerical
underflow (is a condition in a computer program where the result of a
calculation is a number of smaller absolute value than the computer can
actually store in memory.) can occur in floating point numbers. for this reason,
the logarithm is taken of each probability.
The well known identity log(a*b) = log(a)+log(b) is used, so
the final log probability is
This log probability is used as the 'fitness' of a piece of
text, a higher number means it is more likely to be english, while a lower
number means it is less likely to be english.
Here is the code to break the Caesar cipher text:
MODULE 1:
from math import log10
class ngram_score(object):
def __init__(self,ngramfile,sep=' '):
''' load a file containing ngrams and counts, calculate log probabilities '''
self.ngrams = {}
for line in file(ngramfile):
key,count = line.split(sep)
self.ngrams[key] = int(count)
self.L = len(key)
self.N = sum(self.ngrams.itervalues())
#calculate log probabilities
for key in self.ngrams.keys():
self.ngrams[key] = log10(float(self.ngrams[key])/self.N)
self.floor = log10(0.01/self.N)
def score(self,text):
''' compute the score of text '''
score = 0
ngrams = self.ngrams.__getitem__
for i in xrange(len(text)-self.L+1):
if text[i:i+self.L] in self.ngrams: score += ngrams(text[i:i+self.L])
else: score += self.floor
return score
import re
from ngram_score import ngram_score
fitness = ngram_score('english_quadgrams.txt') # load our quadgram statistics
from pycipher import Caesar
def break_caesar(ctext):
# make sure ciphertext has all spacing/punc removed and is uppercase
ctext = re.sub('[^A-Z]','',ctext.upper())
# try all possible keys, return the one with the highest fitness
scores = []
for i in range(26):
scores.append((fitness.score(Caesar(i).decipher(ctext)),i))
return max(scores)
# example ciphertext
fhand = open("encrypt_file.txt",'r')
ctext = fhand.read()
max_key = break_caesar(ctext)
print 'best candidate with key (a,b) = '+str(max_key[1])+':'
print Caesar(max_key[1]).decipher(ctext)
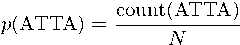
Post a Comment